|
ПОДАРОК ШАМБАЛЫЛетели воздушные корабли. Лился жидкий огонь. Сверкала искра жизни и смерти. Н. К. Рерих. "Письмена"
С Михаилом Николаевичем Новиковым я познакомился в ЦДКЖ во время одного из шахматных турниров. Потом он стал бывать у меня, оказавшись милым, оригинально мыслящим и разносторонним человеком. Шахматы были его страстью. И не просто страстью, а ведущей (вернее сказать, зовущей) идеей. Было ему лет тридцать. Жизнерадостный, деликатный, сын пианиста, он сам неплохо играл на рояле и даже сочинял музыку. Во время легких шахматных партий он признался мне, что верит в существование единого алгоритма шахматной игры, основанного, как ему казалось, не на многомиллионных пересчетах всех возможных вариантов, что доступно лишь электронно-вычислительным машинам, а на некой геометрической основе. Я искренне сомневался в надежности такого подхода, когда даже эвристический метод программирования электронного "гроссмейстера", разрабатываемый прославленным шахматистом и ученым М. М. Ботвинником, должен был бы отступить на второй план. Большинство партий М. Н. Новиков мне проигрывал. Но однажды он запасся бланком для записи партии (серьезных партий с часами я давно не играю, запретив это себе) и попросил у меня разрешения условно ставить фигуру на выбранное поле, геометрически анализировать создавшееся на доске положение и, если потребуется, выбирать другое поле или иную фигуру. Поскольку это был эксперимент, я, конечно, согласился. И представьте - проиграл по всем статьям! Я-то знал, что Михаил Николаевич уже не раз пытался играть со мной по своей "системе", но его хватало лишь на первые ходы, а затем он становился обычным шахматистом, что далеко не всегда приносило ему успех. А тут я чувствовал себя раздавленным неведомой мне машиной, которой в физическом смысле не существовало. Я решил, что просто плохо провел партию и будь на моем месте, скажем, гроссмейстер, партия так не закончилась бы. Михаил Николаевич с редким энтузиазмом уверял меня, что ошибки быть не могло, ибо алгоритм, который он ищет, безусловно, универсален и исходит из самой сути шахмат. Мне хотелось проникнуть в психологию настойчивого искателя, и я осторожно расспрашивал его. Он пообещал принести мне в следующий раз "доказательство", которое убедит меня в его правоте. И однажды он пришел с истрепанной, видавшей виды старой тетрадью, побывавшей и в костре, и в воде, со сморщенными страницами и расплывшимися строчками, даже с обгоревшим углом. Словом, с "документом" весьма романтического вида. С внутренней усмешкой я раскрыл загадочную тетрадь и... перенесся, как в машине времени, на сорок с лишним лет назад... в Нью-Йорк, на Всемирную выставку 1930 года "Мир завтра", в советский ее павильон, в устройстве которого я, как инженер, принимал тогда участие. В его просторных и прохладных в нью-йоркскую жару залах, где звучал набатным колоколом несравненный бас Поля Робсона, исполнявшего "Полюшко, поле" и другие советские песни, я наблюдал множество американцев, пытавшихся увидеть в советском павильоне свой завтрашний день, поскольку в других павильонах им показывали преимущественно рекламу завтрашней продукции различных фирм. Наш павильон представлял собой великолепное подковообразное здание, увенчанное знаменитой статуей рабочего со звездой в поднятой руке. В числе людей, осматривавших павильон снаружи, мне довелось повидать даже английского короля Георга VI, тогда еще не отрекшегося от престола в пользу своей дочери Елизаветы из-за желания жениться не на особе королевской крови, а на американской актрисе. Видел и самого президента Рузвельта с непокрытой головой и внимательными глазами, сидевшего в открытом автомобиле, сопровождаемого конным эскортом. Но теперь перед моим мысленным взором стоял другой посетитель, седой, с белой остроконечной бородкой. Он с выражением спокойной задумчивости на иконописном лице подолгу простаивал перёд экспонатами и старался представить себе, какой стала его любимая Родина после двух преобразивших ее пятилеток. Это был Николай Константинович Рерих, замечательный русский художник, ученый, археолог, этнограф, писатель, поэт, величайший знаток Гималаев, которые он исследовал, организуя экспедиции с ведома молодой Советской республики. Им в равной степени гордятся как в СССР, так и в дружественной нам Индии, ставшей его второй родиной. Если бы я знал, что спустя сорок с лишним лет встречусь с документом, относящимся к одной из его экспедиций и затрагивающем историю любимых мной шахмат, я бы решился подойти к нему, расспросить. Но в те годы ничего этого я не знал. И лишь теперь образ живого Рериха, каким я видел его, предстал передо мной. когда я разбирал полустертые строки ветхой тетради. На первой обгоревшей странице отрывок стихотворения Н. К. Рериха из цикла, названного А. М. Горьким "Письмена":
Дал ли Рерих из России - Примите. Дал ли Аллал-Минг Шри-Нишара из Тибета - Примите.
Многие страницы прочесть было невозможно, но вот... "...Николай Константинович решил писать портрет Учителя, "махатма", как он себя именует, утверждая, что он из Шамбалы, путь куда так настойчиво мы ищем уже который год! Говорят, что дорога в эту сказочную страну мудрецов, мужчин и женщин, живущих общиной, не зная зла и несправедливости, частной собственности и угнетения, откроется якобы только людям с чистой совестью и светлым умом. Неужели это мы, спутники Рериха, почитаемого всеми, кто знал его, мешали ему достичь Шамбалы? Ведь ему-то путь туда несомненно открылся бы! Недаром навстречу вышел этот Учитель, Махатм, вручивший Рериху послание гималайских мудрецов его Родине!" Старый документ взбудоражил мне память. Шамбала! Кто не слышал этого загадочного названия страны, о которой говорят многие, по которую не знает почти никто! Она носит множество имен в различных легендах: Шамбала, Тебу, Беловодье (это у нас в алтайских легендах), Калапа... Но суть страны с этими названиями одна и та же! Обитель мудрецов, ведущих свой род от тех, кто якобы прилетел на Землю из созвездия Ориона. Опи хранят и умножают необыкновенно глубокие знания во всех областях жизни, в особенности в космогонии и законах природы. Эти знания передаются из поколения в поколение. И там есть башня Шамбалы, где хранится камень Чинтамани, доставленный па Землю в шкатулке вместе с тремя другими необыкновенными предметами на "Крылатом копе" Лунг-та, способном пересекать Вселенную (надо думать, па звездолете!). Камень Чинтамани обладает удивительным свойством влиять на человеческую психику, излучая внутренний жар (быть может, радиация?). Отдельные его части, не теряющие якобы связи с основным камнем, появлялись в различных местах земного шара, когда там происходили важнейшие события, начиналась новая эра или зарождалась новая цивилизация. Я словно прикоснулся к этому чудесному камню, когда несколько лет назад вместе со своим другом художником Сергеем Павловичем Викторовым стоял рядом с сыном Николая Константиновича Рериха Николаем Николаевичем перед картиной, на которой его отец воспроизвел доставку камня Чинтамани в башню Шамбалы. Маленький пони несет на себе заветную шкатулку, идя по глубокому ущелью. Сопровождающие его люди знают дорогу к башне Шамбалы, где хранится и ныне чудесный камень. Я почти физически ощущал изображенное Рерихом свечение, излучаемое шкатулкой. И даже Николая Николаевича Рериха, тоже незаурядного художника, с которым познакомились мы с Викторовым, не мог я расспросить о беседе его отца с посланцем Шамбалы, не знал еще об этом! Позже прочел я, что махатм передал Рериху письмо из коммуны гималайских мудрецов правительству молодой Советской республики. Об этом сообщалось в журнале "Международная жизнь" (№ 1, 1965; полный текст послания приведен в творческой биографии Н. К. Рериха, написанной Валентином Сидоровым в книге "На вершинах", изданной в 1977 году). Николай Константинович Рерих привез послание в Советскую Россию и встретился для его передачи с Г. В. Чичериным и А. В. Луначарским. В послании говорилось, что в Гималаях Махатмы знают об уничтожении в новой России частной собственности и власти денег, об упразднении церкви, как рассадника лжи, закрытии притонов. Кончается послание словами: "Привет вам, ищущим общего блага!" Видно, по душе мудрецам Шамбалы пришлись принципы Великой Октябрьской революции, которые потрясли мир. Не ради ли этих принципов ходили в мир посланцы Шамбалы? Они учили жить и предостерегали от катастроф. Не с их ли слов появились в старинных индийских рукописях записи, суть которых не могла быть известна древним жителям Земли. Я приведу несколько переводов с санскритского советского индолога А. Горбовского (в том числе из "Махабхараты"). "Сверкающий снаряд, обладающий сиянием огня, лишенного дыма, был выпущен. Густой туман внезапно покрыл войско. Все стороны горизонта погрузились во мрак. Поднялись несущие зло вихри. Тучи с ревом устремились в высоту неба. Казалось; даже солнце закружилось..." Войско было сожжено, испепелено на месте этим страшным взрывом. Примененное же оружие внешне было похоже на огромную железную стрелу, воспринимаемую как посланца Смерти. Чтобы обезвредить одну такую неиспользованную стрелу, ее требовалось истолочь в порошок и утопить в море. Уцелевшие воины сразу после взрыва должны были спешить к реке, чтобы омыть одежду и оружие (избавиться от радиоактивности?). И об этом писали тысячелетия назад! Чем, как не пересказом пережитых на иных планетах ядерных войн, была эта запись? Как иначе объяснить древнее сообщение о "летательных аппаратах", молниями поражавших с воздуха некий неизвестный в земной истории "Тройной Город"? Не это ли вдохновило поэта Рериха на стихи?
Летели воздушные корабли. Лился жидкий огонь. Сверкала искра жизни и смерти.
Чудовищное оружие, о котором и знать не могли люди в давние времена, тем не менее упоминается в Индии под названием "пламя Индры", в Южной Америке - "оружие Машмак" (фонетически перекликается со словом махатм) и даже в кельтской мифологии как "оружие Грома"... Я оставляю современные легенды о неопознанных летающих объектах (НЛО, УФО), чуть ли не вылетающих из Шамбалы и возвращающихся туда, на совести распространяющих эти россказни, но я все же, опираясь на древние рукописи разных народов, не могу исключить общения мудрецов Шамбалы с древними людьми, не могу не вспомнить их предостережений о грозной опасности, которая ныне, как всем известно, реально висит над всей планетой! То, что Н. К. Рерих считал Шамбалу отнюдь не мифической страной, доказывает его обращение в Наркомат иностранных дел, возглавлявшийся Чичериным, с просьбой о предоставлении "экспедиционного паспорта". Благожелательное с советской стороны отношение к Рериху и его исследовательской деятельности в Гималаях позволило ему посвятить этому важнейшему делу двадцать пять лет своей жизни. Всего лишь об одном дне из этого двадцатипятилетия повествует сейчас потрепанный дневник. Переписываю из него то, что могу разобрать. "Махатм из Шамбалы, угадав желание Рериха написать его портрет, сказал, что он лишь тень мудрости, пославшей его, и не достоин быть увековеченным в красках. Тогда Николай Константинович принял неожиданное решение изобразить Махатма в виде тени на скале. А краски будут вокруг". Отодвигаю дневник. Я ведь видел вместе с Викторовым эту картину! Видел на выставке произведений Н. К. Рериха на Кропоткинской улице в семидесятых годах! Неземное, бледное небо. На его фоне многоцветные, синие и желтоватые скалы. На переднем плане удивительно ровный срез скалы, как бы приваленной к груде исполинских камней. И на этом срезе - отброшенная едва взошедшим солнцем тень старца в ниспадающем одеянии, с остроконечной бородой, напоминающей ту, что носил сам Рерих. Вот оно - документальное доказательство встречи Рериха с гималайским мудрецом, посланцем Шамбалы! Когда картина с тенью на скале была написана, махатм и Рерих уселись друг против друга на корточки. Между ними оказалась шахматная доска с цифрами на каждой клетке и с набором шахматных фигур. Удивительно, но Рерих с махатмом не играли, а рассуждали о математическом квадрате, известном в Индии с древнейших времен как "индийский насик". В Европе лишь спустя тысячелетия появился "магический квадрат", названный так за его необъяснимо волшебные свойства. Одним из позднейших его исследователей стал великий математик XVII века Пьер Ферма. Не знаю, были ли высказанные некоторыми авторами мысли о родстве шахмат с магическим квадратом отголосками беседы Рериха с мудрецом в Гималаях или авторы эти самостоятельно пришли к аналогичным выводам, но для меня важно, что идеи эти уже высказывались. Так, в 1969 году в издательстве "Просвещение" вышла книга Н. Рудина (ждавшая своего издания более сорока лет!), она вызвала весьма противоречивые отклики. А еще в 1929 году в журнале "64, шахматы и шашки в рабочем клубе" появилась статья В. Нейштадта на ту же тему. Понадобилось судебное разбирательство, чтобы установить, что книга Рудина была написана ранее статьи Нейштадта (не указавшего источника). Не моя задача установить этот источник! Я лишь, призывая воображение, переношусь в Гималаи. Горы! Вокруг непостижимо чистый воздух, сквозь который даже далекие предметы кажутся близкими, а цвета скал ничем не смягчены. Вот откуда бралась непостижимая палитра красок Н. К. Рериха! Склоны синие, желтые, резко граничащие, небо малиновое... Такой пейзаж можно представить себе где-нибудь на Марсе с воздухом, разреженным до необычайности! Или на Луне с тенями резкими, как у Рериха, где грани горных образований ничем не сглажены. Два человека, по-разному одетые, но чем-то похожие друг на друга, сидят по обе стороны шахматной доски. Махатм говорит размеренно, неторопливо. Его движения замедленны, но уверенны: - Слава мудрым! Ваши знатоки цифр познали тайны скопления цифр в квадратах. Но напрасно они именуют их "магическими". Магии нет в мире! Нет ее и в цифрах! Все в науках, как и в природе, определяется непреложными законами. Мы, живущие, способны лишь их выявлять. В цифровом квадрате (рис. 1), Для квадрата "насик" с 64 клетками сумма равна 260. Это легко проверить. 1+58+3+60+63+8+6+61=260 или 28+21+12+ +5+36+45+52+61=260. Махатм говорил на превосходном английском языке с безукоризненным произношением, правда, порой растягивая гласные, что придавало его речи певучесть. – Ты не удивишься, мой мудрый друг, когда две соседние двойки дадут в сумме 4. Но расставить цифры в квадрате, чтобы сумма их во всех рядах и диагоналях была постоянной, куда сложнее. Честь вашим знатокам цифр, нашедшим формулы для решения таких задач. Но пока, к сожалению, лишь для квадратов с нечетным числом полей. "Насик" с его 64 клетками можно построить с помощью специальных фигур. – Математических символов? – Скорее "мер", которыми отмеряют расстояние между порядковыми цифрами. У нас в Шамбале поразились, узнав, что наши подсобные математические фигуры послужили для создания великомудрой игры, в которой противоборствуют умы. Восхищения достойна красота, рожденная мудростью. Это закономерно, ибо в основе красоты - порядок, целесообразность, совершенство. А математика со своими фигурами передала игре именно эти свойства. – Какими же были эти старые фигуры? – Им не требовалось иметь те удлиненные ходы, которые придали мудрой игре глубину. Но король (главная фигура) имел доступ ко всем прилегающим к его полю клеткам. Ферзь же ограничивался лишь соседним полем по диагонали. Слон (я применяю ваши, современные названия) был подвижнее и мог ходить через клетку по диагонали. Ладья же - через клетку по горизонтали или вертикали. – А пешка или конь? – Их ходы остались прежними, но пешка не имела права делать два хода с начального поля, а конь не перепрыгивал через фигуры. Не было в этом надобности. Если хочешь, построим "насик" с помощью этих фигур. Ты можешь записать ходы, как это делают шахматисты. – Я слаб в шахматах. Тем более в записи. – У тебя есть помощник с тетрадью. Итак, поставим на a1-1. X
– Итак, мудрый мой друг, "насик" готов наполовину. Не составит труда заполнить и оставшиеся поля. Тогда он отразит бесконечные законы математики. – Бесконечные? – удивился Рерих. – Он и сам станет бесконечным, как Вселенная, надо лишь уподобить его кругу, чтобы он соприкасался сам с собой всеми своими сторонами. – Как это может быть? – Очень просто. Сложи квадрат пополам по вертикальной линии между рядами "d" и "е". Полученную полоску с квадратиками полей сверни трубкой (рис. 2) – Я смотрел на твой перстень, Учитель, и нарисовал его с цифрами на нанесенных квадратиках. – Если бы ты на самом деле увидел на моем перстне цифры, ты принял бы его за талисман? Так знай: суеверие хуже религии, которая хоть в первоначальной форме основывалась на сотворении добра другим. Суеверие служит лишь для тебя самого. – Ты поистине мудр, махатм! – Я лишь тень нашей мудрости, обратившаяся к твоему народу со словами: "Привет вам, ищущим общего блага". И он ушел, оставив Рериха размышлять обо всем услышанном. Ушел, легко перепрыгивая с камня на камень, взбираясь все выше и выше, пока не скрылся исчезающей тенью в тумане, который со дна ущелья казался облаком. На этом закончилась вызванная моим воображением картина, следствие которой, если хотите,, можно рассматривать как гипотезу о чудесном математическом квадрате, что получается с помощью шахматных фигур. Мы с Михаилом Николаевичем достроили его, заглядывая в старую тетрадь и подсчитывая суммы цифр вдоль и поперек, яростно щелкая на счетах, как заправские кассиры. – Ну и что? – спросил я, откидываясь на спинку стула, – бухгалтерия ясна. Но при чем тут ваш алгоритм? А я ведь тайно жаждал реванша с неведомой алгоритмической "машиной". – Как при чем? – вспыхнул Михаил Николаевич. – Алгоритм вытекает из закономерностей, которые вы сейчас увидите. – Какая связь? – пожал я плечами. – Как вы не понимаете! – в отчаянии воскликнул Михаил Николаевич. Мне даже стало жалко моего энтузиаста. Я ведь прикидывался, будто не понимаю, а на самом деле не прочь был овладеть алгоритмом. Чтобы выиграть у любого партнера? Что со мной? Ведь я всегда ценил в шахматах процесс игры, ее красоту, а не результат! Зачем же этот антихудожественный алгоритм? И в состоянии внутренней борьбы узнавал я о преследованиях шахматной жар-птицы. – "Насик", – объяснял Михаил Николаевич, – обладает более совершенными свойствами, чем обычные магические квадраты.
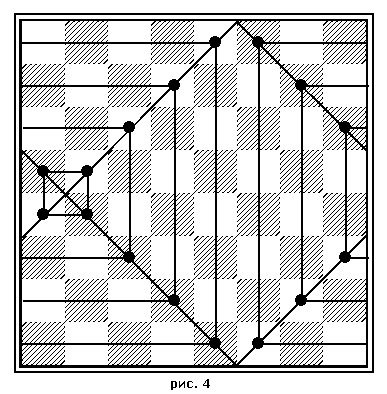
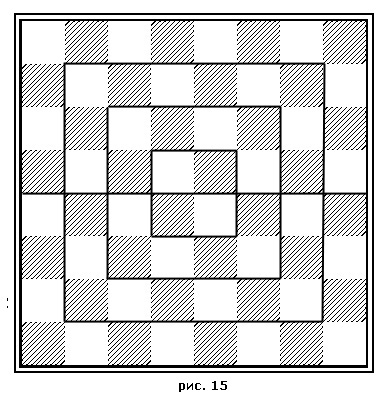
В поисках алгоритма я проверил все...все! "Сейчас проговорится!" - чуть ли не с опаской подумал я, не пропуская ни слова. – В "насике" не только вертикальные и горизонтальные ряды, но также и любые диагонали, так остроумно превращенные махатмом в спирали, дают сумму цифр восьми полей равную 260! Но это далеко не все! Вокруг центрального квадратика из четырех полей (рис. 3) можнопостроить квадраты из 16, 36 и, наконец, из 64 полей. И сумма цифр угловых полей на всех этих квадратах будет 130! И все это построение можно сдвинуть в любую сторону. Ничего не изменится! (рис. 4)
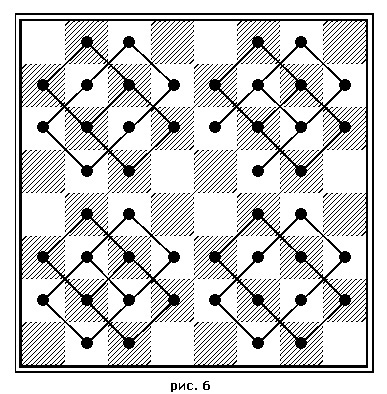
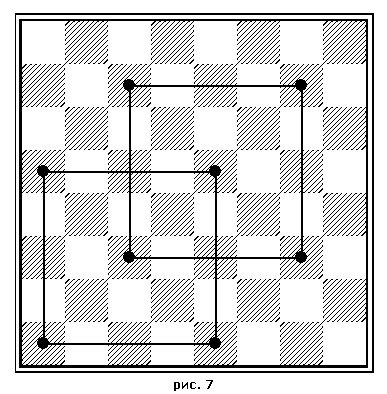
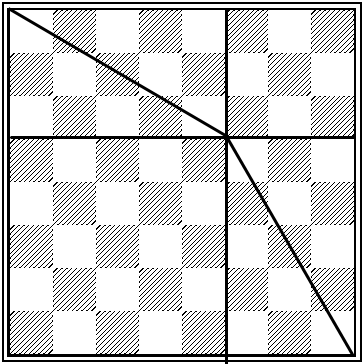
Самое интересное, что на "насик" можно нанести сетку прямоугольную (рис. 5) и сетку диагональную (рис. 6). В узлах, отмеченных на сетках, окажутся определенные цифры. Их сумма в любом квадрате из 2, 4, 6 и 8 полей в стороне всегда равна 130. Но есть еще особый случай: квадрат с пятью полями! (рис. 7) На первом ряду он отмечен полем е1 (на котором, заметим, поставлен белый король!). Это как бы золотое сечение: 5 полей и 3 поля слева и справа в горизонтальном ряду дают суммы два раза по 130! Такую же сумму 130 дают и узловые поля пятипольного квадрата, где бы он ни был расположен в "насике". Диагональная сетка выражена двумя прямоугольниками, - расположенными крест-накрест в каждой четверти (квадрата) "насика". Прямоугольники складываются из двух квадратов каждый.
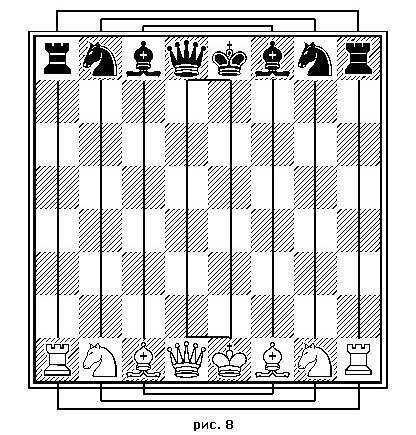
Отмеченные на них узлы приходятся на цифры, которые для каждого диагонального квадрата дают те же 130! – Преклоняюсь перед волшебством. Но при чем тут шахматы? – В том-то и дело, что не только шахматы. Сетка-то напоминает кристаллическую решетку! Но начнем с шахмат. С расстановки фигур (рис. 8). Цифры на полях a1, h1, a8 и h8 в сумме дают 130! Это для ладей! Но то же самое и для слонов: b1, f1, b8, f8, и для коней: b1, g1, b8, g8, и, наконец, для короля и ферзя суммы цифр опять будут 130! Все фигуры занимают целиком ряд с константой 260, точно так же, как и каждый из рядов пешек. – Случайность, – сделанным равнодушием заметил я. – Просто фигуры поставлены в ряд, где цифры подобраны. – Какая же это случайность, когда можно рассмотреть ходы фигур, а не только их первоначальное положение? Король! Вы же заметили, что каждые четыре поля в любом квадратике доски дают сумму цифр 130. А если поставить рядом два таких Квадратика, можно и со сдвигом на одну клетку (или даже на две)?
В восьми полях будет сумма 260! А что это за восемь полей (рис. 9)? Это же поля, которые может последовательно занять король при своих семи ходах! Так что и ему в движении присуща та же константа. Так ведь и с другими фигурами та же история! – Вы так думаете? – Знаю! Ферзь. Поставим его в угол на a1 (рис. 10). Восемь последовательных полей, которые он займет при семи ходах в одном направлении, дадут сумму цифр 260, как в полной диагонали. А если она спиральная, то начинать можно в любом месте "насика" и двигаться в любую сторону. Более того! Если ферзь начнет путешествовать по узлам диагональной сетки, похожей на кристаллическую решетку, то может обойти получившиеся фигуры так, чтобы пройти оба квадрата по восьми полям, что в сумме цифр опять даст 260. Может ферзь пройти и другими путями, которые видны на диаграмме. Ну как? – Совпадение.
– Уже доски? – А что вы скажете о слонах, которые, двигаясь по спиральным диагоналям навстречу друг другу, опять-таки дают константу? Современные ходы лишь облегчают получение константы. Например: 1. Ch8, 2. Сb2, 3. Cg7, 4. СсЗ, 5. Cf6, 6: Cd5, 7. Се5. Остались еще конь и пешки! – Я вас понял. В старом анекдоте во время экзамена поп старался выдавить из семинариста слово "чудо" и спрашивал: "Что это такое, когда человек упал с колокольни и остался жив?" "Случайность", – ответил растерявшийся семинарист. Упрямый поп все наводил семинариста на верный ответ: "Ну, а если второй раз человек упал с колокольни и остался жив? Что это такое?" "Совпадение, ваше преподобие", – еле вымолвил вспотевший семинарист. Поп рассвирепел, затряс гривой: "А ежели в третий раз человек упал с колокольни и жив остался, что это такое? Ответствуй!" Тут семинарист выпрямился и отчеканил: "Привычка!" – и стал несостоявшимся попиком. – Так вы хотите сказать, что с конем и пешкой это уже "привычка"? – вскипел Михаил Николаевич. – Вы все хотите, чтобы я произнес "чудо"? – пытался я улыбкой успокоить его. – Так я вам покажу нечто непривычное. В пифагорову теорему верите? – Я кивнул. – Неверна она тут для коневой диагонали! – Это как же? Ее как будто тоже в Индии доказали. И я вспомнил это доказательство. X
– Опять Шамбала? – Конечно! Все, что я рассказывал, – все из Шамбалы. Так вот! Конь! Коневая диагональ (рис. 12), проведенная через поля, по которым пройдет конь, затронет за один оборот спирали четыре поля и восемь - за два, когда квадрат будет пройден от края до края, сумма цифр при этом будет 130+130=260! И что самое интересное, если строить после трех ходов коня треугольник на его диагонали, как на гипотенузе, с катетами на сторонах квадрата, то сумма цифр гипотенузы будет просто равна сумме цифр малого катета. Вот вам и Пифагор! – Так то сумма цифр, а не длина! Это что-то новое. – Новое - значит непривычное. А вы говорите "привычка"!
Теперь пешки! Выстроенные в ряд, они дают константу. Но если они передвинутся и две из них побьют в разные стороны, то новый ряд снова даст константу (рис. 13). Движение же центральной пешки (рис. 14) - d3-de-ed-d6-d7-d8 дает ту же сумму цифр 260. Или черная пешка а7. Она идет по полям а6-а5-а4-аЗ-Ь2, и теперь взятие или на а1 или на с1. В одном случае сумма цифр будет 259, а в другом 261. В среднем та же константа 260, хотя пешки проходят не восемь, а лишь семь полей. Я еще не признался, не произнес слово "чудо", но оно могло бы произойти, если бы Михаил Николаевич открыл тайну алгоритма. Но он не скрывал ее (если знал!). Увлеченный моей фантазией, он уверял меня, что махатм сказал Рериху много больше, чем я вообразил. Но этого не записано в дневнике.
– Ну, это вы уж слишком! – Нисколько! Число возможных первых ходов фигур и пешек равно числу аминокислот - 20. Если разделить число полей центральных квадратов пополам (рис. 15), то получится ряд: 2-8-18-32. Это равно числу электронов на устойчивых орбитах (в физике!). Махатмы все знали, все! 2, 8, 18, 32 и обратно 32, 18, 8, 2 - строение оболочек элементов (химия!). – Почему же этого нет в дневнике? – Потому что автор записи ничего в этом не понимал. – А что это за сакраментальные цифры 260 и 64? – 64! Это 4 в кубе! 4 - символизирует аденин (А), гуанин (Г), цитозин (Ц) и тимин (Т). Для 20 аминокислот, требуемых человеку, нужны 64 тройки оснований, так как код их триплетен. Необходимо 43=64. Кстати, 260=4х65, а 65 - сумма угловых цифр по диагоналям четырех квадратов "насика". 1+64, 28+37, 40+25, 61+4! И еще... Михаила Николаевич – Это двойная спираль биологического кода, - объяснял он, - с числом полей по большой диагонали - 2, 8, 18, 32! Это как бы 32 группы симметрии в кристаллографии. Кстати, вспомните сетку на "насике", так напоминающую кристаллическую решетку. Или кристаллические фигуры диагональных квадратов! Но двойвая спираль еще и астрономический символ, скажем, схема строения галактик. Но вернемся к учению о жизни. Заметим, что ДНК - это АГЦТ, РНК - АГЦУ. У - урацил - аналог тимина. Строение ДНК и РНК, то есть дезоксирибонуклеиновая и рибонуклеиновая кислоты, составляющие основу наследственного кода любого существа: и комара, и слона, и человека-по своему строению одинаковы и отражены (пусть символически) в шахматах! – Сдаюсь! – поднял я руки. – Остановите часы. Впрочем, с часами я не играю. Одно мне ясно, если шахматы хоть в какой-то мере зиждятся на математических или биологических основах, то... – И астрономических! космических! Они отражают химические реакции, ядерный процесс, синтез белка, рождение и смерть звезд!.. – Стоп, стоп, стоп! Как же вы можете искать алгоритм шахмат? Вы же убьете их! – Почему же? Подъемные краны и экскаваторы не уничтожили тяжелую атлетику. Алгоритм пригодится и в теории шахмат, и при анализах. И, может быть, заставит шахматистов искать пути сохранения единоборства. Скажем, так изменить регламент игры, чтобы заканчивать партию за один прием. Разве не лучше, чтобы в состязании участвовали только сами шахматисты-соперники, а не их команды секундантов и помощников. – Мысль не нова. Ее выдвигал еще гроссмейстер Давид Бронштейн. Разве что угроза применения вашего алгоритма поможет? Честное слово, я боюсь, что он умертвит живую мудрую игру. И вам ли, покушающемуся своим алгоритмом на основу шахматной борьбы, печься о чистоте единоборства шахматистов, обязанных торопливо закончить партию в один прием? Что ж, публикуйте тогда свой алгоритм. Публикуйте! – Не раньше чем выиграю у гроссмейстера. – Благодарю вас за оценку проигранной мной партии. – Но она же была экспериментальная, – попытался он утешить меня. – Нет, нет! Я вполне согласен с вашей оценкой моей игры. Но я от души благодарю вас за этот эксперимент. – А я благодарю за Махатма, за беседу Рериха с ним. За то, что сумели убедить меня в причастности шахмат к объективным законам математики и природы. Может быть, потому они так жизненны? Я не боюсь применить к ним желанное вами слово "чудо".
|
будем так называть его, числа расставлены в расчете, что их сумма в любом горизонтальном или вертикальном ряду всегда одна и та же.
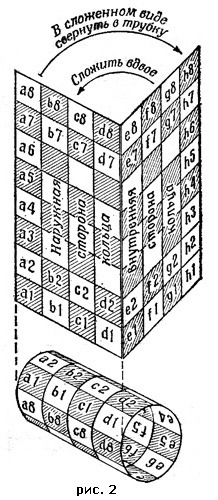и получишь кольцо. Поле а1 соседствует в нем с полем h1, на переходе с внешней стороны кольца на внутреннюю. Первый же горизонтальный ряд соприкасается с восьмым на обеих сторонах кольца. Как видишь, квадрат может примыкать к самому себе всеми сторонами. Я замечаю, ты все понял и даже нарисовал получившуюся фигуру в тетради ученика.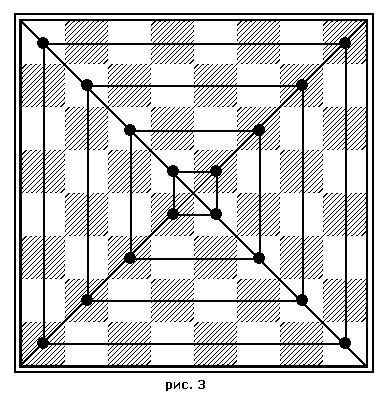
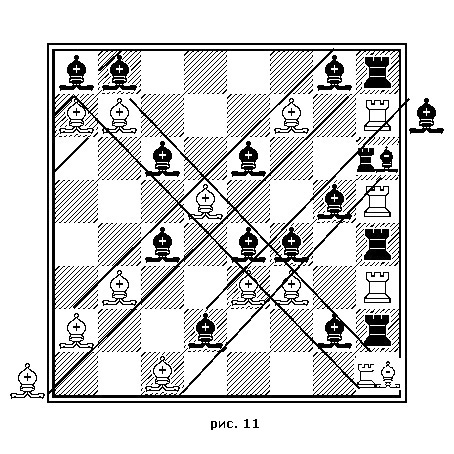– Тогда что вы скажете о ладьях (рис. 11)? Двигаясь навстречу друг другу в любом месте "насика", они займут весь ряд с его константой 260. Современные ладьи дают тот же результат и без встречного движения. Причем ладья может начинать с любого поля доски.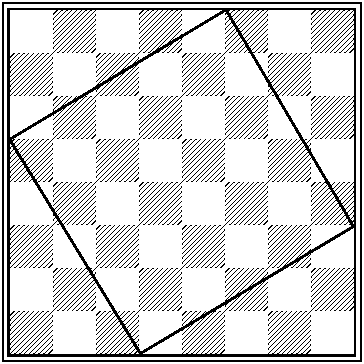
– Тем не менее в шахматах отражены не только математические, но и биологические константы. Одно сходство слов: "шахматы" и "махатмы" чего стоит!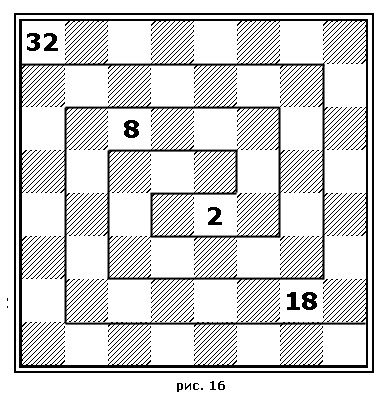
а уже невозможно было остановить. Он рисовал в "насике" спираль (рис. 16).